मोंटेसरी विधि, दूसरा संस्करण - बहाली # अध्याय 19 - अंकगणित का शिक्षण, अंकगणित का परिचय तीन साल के बच्चे पहले से ही जानते हैं कि जब वे हमारे स्कूलों में प्रवेश करते हैं तो दो या तीन तक कैसे गिनें। इसलिए वे  ***बहुत आसानी से***  अंकगणित सीखते हैं, जिसमें  ***वस्तुओं को गिनना** शामिल है ।*  एक दर्जन अलग-अलग तरीके इस दिशा में काम कर सकते हैं, और दैनिक जीवन कई अवसर प्रस्तुत करता है; जब माँ कहती है, उदाहरण के लिए, "आपके एप्रन से दो बटन गायब हैं," या "हमें टेबल पर तीन और प्लेट चाहिए।" मेरे द्वारा उपयोग किए जाने वाले पहले साधनों में से एक पैसे से गिनने का है। मुझे  ***नया***  पैसा मिलता है, और यदि यह संभव हो तो मुझे कार्डबोर्ड में अच्छे प्रतिकृतियां बनानी चाहिए। मैंने लंदन के एक स्कूल में इस तरह के पैसे का इस्तेमाल कमियों के लिए होते देखा है। परिवर्तन  करना अंक ***का***  एक रूप है जो इतना आकर्षक है कि बच्चे का ध्यान आकर्षित करता है। मैं एक, दो और चार सेंटीमीटर के टुकड़े प्रस्तुत करता हूं, और बच्चे इस तरह से  ***दस तक गिनना सीखते हैं** तक गिनना सीखते हैं ।* ***बच्चों को आम उपयोग में आने वाले सिक्कों से परिचित कराने की प्रवृत्ति से अधिक व्यावहारिक*** शिक्षा का कोई भी रूप नहीं है   , और कोई भी व्यायाम परिवर्तन करने से अधिक उपयोगी नहीं है। यह दैनिक जीवन से इतना घनिष्ठ रूप से जुड़ा है कि यह सभी बच्चों को गहनता से आकर्षित करता है। इस अनुभवजन्य विधा में अंकन सिखाने के बाद, मैं और अधिक पद्धतिगत अभ्यासों को पास करता हूं, जिसमें पहले से ही इंद्रियों की शिक्षा में उपयोग किए जाने वाले ब्लॉकों के सेटों में से एक उपदेशात्मक सामग्री है; अर्थात्, लंबाई के शिक्षण के लिए पहले इस्तेमाल की गई दस छड़ों की श्रृंखला। इनमें से सबसे छोटी छड़ एक डेसीमीटर से मेल खाती है, सबसे लंबी एक मीटर से, जबकि बीच की छड़ें एक डेसीमीटर लंबाई के वर्गों में विभाजित होती हैं। वर्गों को बारी-बारी से लाल और नीले रंग में रंगा गया है।  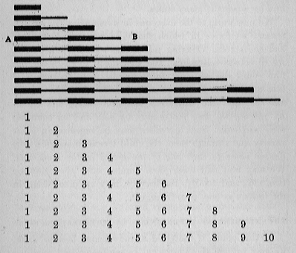किसी दिन, जब एक बच्चे ने छड़ों को लंबाई के क्रम में रखकर व्यवस्थित किया है, तो हमने उसे सबसे छोटे टुकड़े से शुरू होने वाले लाल और नीले संकेतों की गणना की है; वह एक है; एक दो; एक, दो, तीन, आदि, हमेशा प्रत्येक छड़ की गिनती में एक पर वापस जा रहे हैं, और पक्ष ए से शुरू करते हैं। फिर हमने उसे वर्गों की कुल संख्या के अनुसार सबसे छोटी से सबसे लंबी तक की एकल छड़ का नाम दिया है जिसमें प्रत्येक में, बी की ओर की छड़ों को छूते हुए, जिस तरफ सीढ़ी चढ़ती है। इसका परिणाम उसी संख्या में होता है जब हमने सबसे लंबी छड़ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 की गणना की थी। छड़ों की संख्या जानने के लिए, हम उन्हें पक्ष A से गिनते हैं और वही अंक परिणाम; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. अब हम संख्या में अभ्यासों  को पहले के, संवेदी अभ्यासों के साथ ***जोड़ते***  हैं जिसमें बच्चे ने लंबी और छोटी छड़ों को पहचाना। एक कालीन पर छड़ें मिलाने के बाद, निर्देशक एक का चयन करता है, और इसे बच्चे को दिखाता है, क्या उसने वर्गों की गिनती की है; उदाहरण के लिए, 5. फिर वह उससे आगे की लंबाई देने के लिए कहती है। वह इसे  ***अपनी आंख से चुनता है, और निर्देशक ने दो टुकड़ों को एक साथ रखकर और उनके वर्गों*** को गिनकर   अपनी पसंद को  ***सत्यापित** किया है । **इस तरह के अभ्यासों को बड़ी संख्या में दोहराया जा सकता है और उनके माध्यम से, बच्चा लंबी सीढ़ी में प्रत्येक टुकड़े को***  एक विशेष नाम देना सीखता है  । ***।*** **अब हम उन्हें पीस नंबर एक कह सकते हैं; टुकड़ा संख्या दो, आदि, और अंत में, संक्षिप्तता के लिए, पाठों में उनके बारे में एक, दो, तीन, आदि के रूप में बोल सकते हैं।** ## [19.1 संख्याएँ जैसा कि ग्राफिक संकेतों द्वारा दर्शाया गया है](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.1-numbers-as-represented-by-graphic-signs 'मोंटेसरी से लिंक करें। ज़ोन का अनुवाद बेस टेक्स्ट "द मोंटेसरी मेथड"') इस बिंदु पर, यदि बच्चा पहले से ही लिखना जानता है, तो हम सैंडपेपर में कटे हुए और कार्डों पर लगाए गए आंकड़े प्रस्तुत कर सकते हैं। इन्हें प्रस्तुत करने में अक्षरों को पढ़ाने की विधि समान है। "यह एक है।" "यह दो है।" "मुझे एक दे दो।" "मुझे दो दो।" "यह कौन सा  *नंबर*  है?" बच्चा अपनी उंगली से नंबर ट्रेस करता है जैसे उसने अक्षरों को किया था। ***संख्याओं के साथ व्यायाम** ।*  मात्रा के साथ ग्राफिक साइन का जुड़ाव। मैंने दो ट्रे डिज़ाइन की हैं, जिनमें से प्रत्येक को पाँच छोटे डिब्बों में विभाजित किया गया है। प्रत्येक डिब्बे के पीछे एक आकृति वाला एक कार्ड रखा जा सकता है। पहली ट्रे में अंक 0, 1, 2, 3, 4 और दूसरे में 5, 6, 7, 8 और 9 होने चाहिए। व्यायाम स्पष्ट है; इसमें डिब्बों के भीतर कुछ वस्तुओं को डिब्बे के पीछे कार्ड पर दर्शाए गए चित्र के अनुरूप रखना शामिल है। हम बच्चों को पाठ में बदलाव करने के लिए विभिन्न वस्तुएं देते हैं, लेकिन मुख्य रूप से लकड़ी के बड़े खूंटे का उपयोग इस तरह से करते हैं कि वे डेस्क से लुढ़कें नहीं। हम इनमें से कई को उस बच्चे के सामने रखते हैं जिसका हिस्सा उन्हें उनके स्थानों पर व्यवस्थित करना है, एक कार्ड के अनुरूप एक खूंटी, आदि। जब वह समाप्त कर लेता है तो वह अपनी ट्रे को निर्देशक के पास ले जाता है ताकि वह अपने काम को सत्यापित कर सके। ***शून्य पर सबक** ।*  हम तब तक प्रतीक्षा करते हैं जब तक कि बच्चा शून्य चिह्नित कार्ड वाले डिब्बे की ओर इशारा करते हुए पूछता है, "और मुझे यहाँ क्या रखना चाहिए?" हम तब उत्तर देते हैं, "कुछ नहीं; शून्य कुछ भी नहीं है।" लेकिन अक्सर यह काफी नहीं होता है। ***बच्चे को यह महसूस*** कराना जरूरी है  कि हमारा क्या मतलब  ***है** ।*  इसके लिए हम छोटे-छोटे खेलों का उपयोग करते हैं जो बच्चों का भरपूर मनोरंजन करते हैं। मैं उनके बीच खड़ा हूं, और उनमें से एक की ओर मुड़ते हुए, जो पहले से ही इस सामग्री का उपयोग कर चुका है, मैं कहता हूं, "आओ, प्रिय, मेरे पास  ***शून्य***  बार आओ।" बच्चा लगभग हमेशा मेरे पास आता है, और फिर अपने स्थान पर वापस चला जाता है। "लेकिन, मेरे लड़के, तुम  ***एक***  बार आए थे, और मैंने तुम्हें आने के लिए कहा था  ***शून्य आने के लिए कहा था*** बार।" फिर वह आश्चर्य करने लगता है। "लेकिन मुझे क्या करना चाहिए?" "कुछ नहीं; शून्य कुछ भी नहीं है।" "लेकिन मैं कुछ नहीं कैसे करूं?" "कुछ मत करो। आपको स्थिर बैठना चाहिए। आपको बिल्कुल नहीं आना चाहिए, किसी भी समय नहीं। शून्य बार। कोई समय नहीं।" मैं इन अभ्यासों को तब तक दोहराता हूं जब तक बच्चे समझ नहीं जाते हैं, और जब मैं उन्हें शून्य बार मेरे पास आने या मुझे शून्य चुंबन देने के लिए कहता हूं, तो वे चुप रहने पर बहुत खुश होते हैं। वे अक्सर रोते हैं, "शून्य है कुछ नहीं! शून्य कुछ भी नहीं है!" ## [19.2 संख्याओं को याद रखने के लिए व्यायाम](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.2-exercises-for-the-memory-of-numbers 'मोंटेसरी से लिंक करें। ज़ोन का अनुवाद बेस टेक्स्ट "द मोंटेसरी मेथड"') जब बच्चे लिखित आकृति को पहचानते हैं, और जब यह आंकड़ा उनके लिए संख्यात्मक मान को दर्शाता है, तो मैं उन्हें निम्नलिखित अभ्यास देता हूं: मैंने पुराने कैलेंडर से आंकड़े काट दिए और उन्हें कागज की पर्चियों पर रख दिया, जिन्हें बाद में मोड़कर एक बॉक्स में गिरा दिया गया। बच्चे पर्चियों को बाहर निकालते हैं और उन्हें अभी भी मुड़े हुए, अपनी सीटों पर ले जाते हैं, जहाँ वे उन्हें देखते हैं और  ***रहस्य को** बनाए रखते हुए उन्हें वापस कर देते हैं ।*  फिर, एक-एक करके, या समूहों में, ये बच्चे (जो स्वाभाविक रूप से कक्षा में सबसे बड़े हैं) निर्देशक की बड़ी मेज पर जाते हैं जहाँ विभिन्न छोटी वस्तुओं के समूह रखे गए हैं। प्रत्येक व्यक्ति   अपने द्वारा खींची गई संख्या के अनुरूप वस्तुओं की ***मात्रा का चयन करता है।*** इस बीच, नंबर  ***को बच्चे के घर पर छोड़ दिया गया है*** , कागज की एक पर्ची रहस्यमय तरीके से मुड़ी हुई है। इसलिए बच्चे को  ***याद रखना चाहिए*** उसकी संख्या न केवल आने-जाने में होने वाली गतिविधियों के दौरान, बल्कि जब वह अपने टुकड़ों को इकट्ठा करता है, तो उन्हें एक-एक करके गिनता है। निर्देशक यहाँ संख्या स्मृति पर दिलचस्प व्यक्तिगत अवलोकन कर सकता है। जब बच्चा अपनी वस्तुओं को इकट्ठा कर लेता है, तो वह उन्हें अपनी मेज पर दो के कॉलम में व्यवस्थित करता है, और यदि संख्या असमान है, तो वह विषम टुकड़े को नीचे और अंतिम दो वस्तुओं के बीच रखता है। इसलिए टुकड़ों की व्यवस्था इस प्रकार है: ``` o o o o o o o o o o X XX XX XX XX XX XX XX XX XX X XX XX XX XX XX XX XX X XX XX XX XX XX X XX XX XX X XX ``` क्रॉस वस्तुओं का प्रतिनिधित्व करते हैं, जबकि सर्कल मुड़ी हुई पर्ची के लिए खड़ा होता है जिसमें आकृति होती है। अपनी वस्तुओं को व्यवस्थित करने के बाद, बच्चा सत्यापन की प्रतीक्षा कर रहा है। निर्देशक आता है, पर्ची खोलता है, संख्या पढ़ता है, और टुकड़ों को गिनता है। जब हम पहली बार इस खेल को खेलते थे तो अक्सर ऐसा होता था कि बच्चों ने  कार्ड पर बुलाए जाने की तुलना में ***अधिक वस्तुएं*** लीं  , और यह हमेशा इसलिए नहीं था क्योंकि उन्हें संख्या याद नहीं थी, लेकिन वस्तुओं की सबसे बड़ी संख्या होने के लिए उन्माद से उत्पन्न हुई थी। उस सहज लालच का थोड़ा सा, जो आदिम और असंस्कृत मनुष्य के लिए सामान्य है। निर्देशक बच्चों को यह समझाने की कोशिश करता है कि उन सभी चीजों को डेस्क पर रखना बेकार है और खेल का उद्देश्य वस्तुओं की सही संख्या लेने में है। धीरे-धीरे, वे इस विचार में प्रवेश करते हैं, लेकिन इतना आसान नहीं है जितना कोई सोच सकता है। यह आत्म-अस्वीकृति का एक वास्तविक प्रयास है जो बच्चे को निर्धारित सीमा के भीतर रखता है और उसे अपने निपटान में रखी गई वस्तुओं में से केवल दो वस्तुओं को लेने के लिए मजबूर करता है, जबकि वह दूसरों को अधिक लेते हुए देखता है। इसलिए, मैं इस खेल को अंक की तुलना में इच्छाशक्ति का अधिक अभ्यास मानता हूं। जिस बालक के पास  ***शून्य है*** , उसे अपने स्थान से तब नहीं हिलना चाहिए जब वह अपने सभी साथियों को उठकर उन वस्तुओं से मुक्त हो जाता है जो उसके लिए दुर्गम हैं। कई बार शून्य उस बच्चे पर पड़ता है जो पूरी तरह से गिनना जानता है, और जो अपनी मेज पर वस्तुओं के एक अच्छे समूह को उचित क्रम में जमा करने और व्यवस्थित करने में और सुरक्षा के साथ शिक्षक के सत्यापन की प्रतीक्षा में बहुत खुशी का अनुभव करेगा। उन लोगों के चेहरे पर भावों का अध्ययन करना सबसे दिलचस्प है जिनके पास शून्य है। व्यक्तिगत मतभेद जिसके परिणामस्वरूप लगभग हर एक के "चरित्र" का रहस्योद्घाटन होता है। कुछ अधीर रहते हैं, निराशा के दर्द को छिपाने के लिए एक साहसिक मोर्चा मानते हैं; अन्य लोग इस निराशा को अनैच्छिक इशारों से दिखाते हैं। फिर भी, अन्य लोग उस मुस्कान को छिपा नहीं सकते जो उस विलक्षण स्थिति से उत्पन्न होती है जिसमें वे स्वयं को पाते हैं, और जो उनके मित्रों को जिज्ञासु बना देगा। बहुत कम लोग होते हैं जो अपने साथियों की हर हरकत को इच्छा की दृष्टि से, लगभग ईर्ष्या की दृष्टि से देखते हैं, जबकि अन्य स्थिति को तुरंत स्वीकार कर लेते हैं। वे भाव भी कम दिलचस्प नहीं हैं जिनके साथ वे सत्यापन के दौरान पूछे जाने पर शून्य धारण करने की बात स्वीकार करते हैं, "और आपने, आपने कुछ नहीं लिया?" "मेरे पास शून्य है।" "यह शून्य है।" ये सामान्य शब्द हैं, लेकिन अभिव्यंजक चेहरा और आवाज का स्वर व्यापक रूप से भिन्न भावनाओं को दर्शाता है। वास्तव में, वे दुर्लभ हैं जो किसी असाधारण तथ्य की व्याख्या खुशी से देते प्रतीत होते हैं। बड़ी संख्या या तो दुखी दिखती है या केवल इस्तीफा दे देती है। इसलिए, हम खेल के अर्थ पर यह कहते हुए सबक देते हैं, "शून्य रहस्य रखना कठिन है। कागज को कसकर मोड़ो और इसे फिसलने न दें। यह सबसे कठिन है।" दरअसल, थोड़ी देर के बाद, बच्चों को चुप रहने की बहुत कठिनाई होती है, और जब वे शून्य चिह्नित पर्ची खोलते हैं तो यह देखा जा सकता है कि वे रहस्य रखने के लिए संतुष्ट हैं। ## [19.3 एक से बीस का जोड़ और घटाव: गुणा और भाग](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.3-addition-and-subtraction-from-one-to-twenty%3A-multiplication-and-division 'मोंटेसरी से लिंक करें। ज़ोन का अनुवाद बेस टेक्स्ट "द मोंटेसरी मेथड"') पहले अंकगणितीय संक्रियाओं के शिक्षण के लिए हम जिस उपदेशात्मक सामग्री का उपयोग करते हैं, वह वही है जो पहले से ही अंकगणित के लिए उपयोग की जाती है; यानी, छड़ें लंबाई के रूप में स्नातक की जाती हैं, जो मीटर के पैमाने पर व्यवस्थित होती हैं, जिसमें दशमलव प्रणाली का पहला विचार होता है। जैसा कि मैंने कहा है, छड़ों को उन संख्याओं द्वारा बुलाया गया है जिन्हें वे प्रतिनिधित्व करते हैं; एक, दो, तीन, आदि। उन्हें लंबाई के क्रम में व्यवस्थित किया जाता है, जो संख्या के क्रम में भी होता है। पहले अभ्यास में छोटे टुकड़ों को एक साथ इस तरह से जोड़ने की कोशिश करना शामिल है कि दसियों का निर्माण हो। ऐसा करने का सबसे सरल तरीका है कि एक के बाद एक छोटी से छोटी छड़ें लें और उन्हें नौ से नीचे की ओर से संबंधित लंबी छड़ों के अंत में रखें। यह आज्ञाओं के साथ हो सकता है, "एक लो और इसे नौ में जोड़ो; दो लो और इसे आठ में जोड़ो; तीन लो और इसे सात में जोड़ो; चार लो और इसे छह में जोड़ें।" इस तरह हम चार छड़ें दस के बराबर बनाते हैं। पाँच रहते हैं, लेकिन, इसे अपने सिर पर घुमाते हुए (लंबे अर्थ में), यह दस के एक छोर से दूसरे छोर तक जाता है, और इस तरह इस तथ्य को स्पष्ट करता है कि दो गुना पांच दस बनाता है. इन अभ्यासों को दोहराया जाता है और धीरे-धीरे बच्चे को अधिक तकनीकी भाषा सिखाई जाती है; नौ जमा एक दस के बराबर होता है, आठ जमा दो बराबर दस, सात जमा तीन बराबर दस, छह जमा चार बराबर दस, और पांच के लिए, जो दो गुना पांच बराबर दस होता है। अंत में, अगर वह लिख सकता है, तो हम संकेतों को  *प्लस*  और  *बराबर*  और  *समय सिखाते हैं।*  फिर हम अपने छोटों की साफ-सुथरी नोटबुक में यही देखते हैं: ``` 9+1=10 8+2=10 5x2=10 7+3=10 6+4=10 ``` जब यह सब अच्छी तरह से सीख लिया जाता है और बच्चों द्वारा बहुत खुशी के साथ कागज पर डाल दिया जाता है, तो हम उनका ध्यान उस काम की ओर आकर्षित करते हैं जो तब किया जाता है जब दसियों को एक साथ समूहीकृत करके दसियों को अलग कर दिया जाता है और वापस अपनी मूल स्थिति में रख दिया जाता है। अंतिम गठित दस में से हम चार और छह अवशेष निकालते हैं; अगले से, हम तीन और सात अवशेष निकालते हैं; अगले से, दो और आठ अवशेष; आखिरी से, हम एक और नौ अवशेष निकालते हैं। इसे ठीक से बोलते हुए हम कहते हैं, दस कम चार बराबर छह; दस कम तीन बराबर सात; दस कम दो बराबर आठ; दस कम एक नौ के बराबर होता है। शेष पांच के संबंध में, यह दस का आधा है, और लंबी छड़ को दो में काटने से, जो दस को दो से विभाजित कर रहा है, हमारे पास पांच होंगे; दस को दो से विभाजित करने पर पाँच बराबर होता है। इन सबका लिखित रिकॉर्ड पढ़ता है: ``` 10-4=6 10-3=7 10 / 2=5 10-2=8 10-1=9 ``` एक बार जब बच्चे इस अभ्यास में महारत हासिल कर लेते हैं तो वे इसे स्वतः ही गुणा कर देते हैं। क्या हम तीन को दो तरह से बना सकते हैं? हम एक को दो के बाद रखते हैं और फिर लिखते हैं, ताकि हमें याद रहे कि हमने 2+1=3 क्या किया है। क्या हम चार की संख्या के बराबर दो छड़ें बना सकते हैं? 3+1=4, और 4-3=1; 4-1 = 3। रॉड नंबर दो के संबंध में रॉड नंबर चार को दस के संबंध में पांच माना जाता है; यानी, हम इसे पलट देते हैं और दिखाते हैं कि यह चार ठीक दो बार में समाहित है: 4/2=2; 2x2 = 4। एक और समस्या: आइए देखें कि हम एक ही खेल को कितनी छड़ों से खेल सकते हैं। हम इसे तीन और छह के साथ, और चार और आठ के साथ कर सकते हैं; वह है, ``` 2x2=4 3x2=6 4x2=8 5x2=10 10/2=5 8/2=4 6/2=3 4/2=2 ``` इस बिंदु पर हम पाते हैं कि जिन घनों के साथ हमने संख्या स्मृति खेल खेले हैं वे मददगार हैं:  इस व्यवस्था से, कोई तुरंत देखता है कि कौन सी संख्याएं हैं जिन्हें दो से विभाजित किया जा सकता है जिनके नीचे एक विषम घन नहीं है। ये  ***सम***  संख्याएं हैं क्योंकि इन्हें जोड़े में व्यवस्थित किया जा सकता है, दो बटा दो; और दो से भाग करना आसान है, केवल दो पंक्तियों की दो पंक्तियों को अलग करना आवश्यक है जो एक के नीचे एक खड़ी हैं। प्रत्येक फ़ाइल के घनों को गिनने पर हमारे पास भागफल होता है। आदिम संख्या को पुनः संयोजित करने के लिए हमें केवल दो फाइलों को 2x3 = 6 को फिर से इकट्ठा करने की आवश्यकता है। पांच साल के बच्चों के लिए यह सब मुश्किल नहीं है। दोहराव जल्द ही नीरस हो जाता है, लेकिन अभ्यास को सबसे आसानी से बदला जा सकता है, लंबी छड़ों के सेट को फिर से लेना, और नौ के बाद एक नंबर रखने के बजाय इसे दस के बाद रखें। इसी तरह नौ के बाद दो और आठ के बाद तीन लगाएं। इस प्रकार हम दस से अधिक लम्बाई की छड़ें बनाते हैं; लंबाई जिसे हमें ग्यारह, बारह, तेरह, आदि नाम देना सीखना चाहिए, जहाँ तक बीस है। इन उच्च संख्याओं को ठीक करने के लिए छोटे घनों का भी उपयोग किया जा सकता है दस के माध्यम से संचालन सीखने के बाद, हम बिना किसी कठिनाई के बीस तक आगे बढ़ते हैं। ***एक कठिनाई दशमलव संख्याओं*** में निहित है   जिसके लिए कुछ पाठों की आवश्यकता होती है। ## [19.4 दशमलव पर पाठ: दस के बाद अंकगणितीय परिकलन](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.4-lessons-on-decimals%3A-arithmetical-calculations-beyond-ten 'मोंटेसरी से लिंक करें। ज़ोन का अनुवाद बेस टेक्स्ट "द मोंटेसरी मेथड"') आवश्यक उपदेशात्मक सामग्री में कई वर्ग कार्ड होते हैं जिन पर संख्या दस बड़े प्रकार में मुद्रित होती है, और अन्य आयताकार कार्ड, वर्ग के आधे आकार के होते हैं, और एक से नौ तक एकल संख्याएं होती हैं। हम संख्याओं को एक पंक्ति में रखते हैं; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10। फिर, कोई और संख्या न होने पर, हमें फिर से शुरू करना चाहिए और फिर से 1 लेना चाहिए। यह 1 छड़ों के सेट में उस खंड की तरह है, जो छड़ संख्या 10 में, नौ से आगे तक फैला हुआ है। ***सीढ़ी*** के साथ गिनती  **जहां तक ​​नौ है, यह एक खंड बना हुआ है, क्योंकि कोई और संख्या नहीं है, हम फिर से 1 के रूप में नामित करते हैं; लेकिन यह पहले की तुलना में अधिक 1 है, और इसे पहले से अलग करने के लिए हम इसके पास एक शून्य डालते हैं, एक संकेत जिसका कोई मतलब नहीं है। यहां 10 है। अलग-अलग आयताकार संख्या कार्डों के साथ शून्य को कवर करना उनके उत्तराधिकार के क्रम में हम देखते हैं: 11, 12, 13, 14, 15, 16, 17, 18, 19। इन संख्याओं को रॉड में जोड़कर बनाया गया है संख्या 10, पहली-छड़ी संख्या 1, फिर 2, फिर 3, आदि, जब तक कि हम अंत में छड़ संख्या 9 को छड़ संख्या 10 में नहीं जोड़ते, इस प्रकार एक बहुत लंबी छड़ प्राप्त होती है, जिसे बारी-बारी से लाल और नीले वर्गों को गिना जाता है, देता है हमें उन्नीस।**  निर्देशक तब बच्चे को कार्ड दिखा सकता है, 16 नंबर दे सकता है, और वह रॉड 10 के बाद रॉड 6 रख सकता है। वह फिर 6 वाले कार्ड को हटा देती है, और शून्य पर 8 अंक वाले कार्ड को रखती है, जिस पर बच्चा रॉड 6 को निकालता है और इसे रॉड 8 से बदल देता है, इस प्रकार 18 बनाता है। इनमें से प्रत्येक कार्य को इस प्रकार दर्ज किया जा सकता है: 10+6=16; 10+8=18, आदि। हम घटाव के लिए उसी तरह आगे बढ़ते हैं। 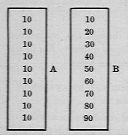जब संख्या का बच्चे के लिए स्पष्ट अर्थ होना शुरू हो जाता है, तो संयोजन एक लंबे कार्ड पर बनाए जाते हैं, जो आयताकार कार्डों को नौ अंकों वाले दो स्तंभों पर आंकड़े ए और बी में दिखाए गए हैं। कार्ड ए पर हम दूसरे 10 के शून्य पर, 1 को प्रभावित करने वाला आयताकार कार्ड, और इसके तहत दो, आदि वाले एक पर आरोपित करते हैं। इस प्रकार दस में से एक समान रहता है, दाईं ओर की संख्या शून्य से नौ तक आगे बढ़ती है, इस प्रकार:  कार्ड बी में आवेदन अधिक जटिल हैं। कार्ड दसियों द्वारा संख्यात्मक प्रगति में लगाए गए हैं। हमारे लगभग सभी बच्चे 100 तक गिने जाते हैं, एक संख्या जो उन्हें सीखने के संबंध में दिखाई गई जिज्ञासा के जवाब में दी गई थी। मैं नहीं मानता कि शिक्षण के इस चरण में और दृष्टांतों की आवश्यकता है। प्रत्येक शिक्षक सरल वस्तुओं का उपयोग करके अंकगणितीय संक्रियाओं में व्यावहारिक अभ्यासों को गुणा कर सकता है, जिन्हें बच्चे आसानी से संभाल सकते हैं और विभाजित कर सकते हैं। > ##### **इस पृष्ठ का लाइसेंस:** > > यह पृष्ठ " **मॉन्टेसरी बहाली और अनुवाद परियोजना** " का हिस्सा है।\ > कृपया हमारी " **सभी के लिए सभी समावेशी मोंटेसरी शिक्षा 0-100+ दुनिया भर में** " पहल [का समर्थन करें। ](https://ko-fi.com/montessori)हम मोंटेसरी शिक्षा में रुचि रखने वाले सभी लोगों के लिए खुले, मुफ़्त और किफायती संसाधन उपलब्ध कराते हैं। हम लोगों और वातावरण को दुनिया भर में प्रामाणिक मोंटेसरी के रूप में बदलते हैं। धन्यवाद! > > [](http://creativecommons.org/licenses/by-nc-sa/4.0/) > > **लाइसेंस: यह कार्य अपने सभी पुनर्स्थापन संपादनों और अनुवादों के साथ एक** [Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International लाइसेंस](http://creativecommons.org/licenses/by-nc-sa/4.0/) के अंतर्गत लाइसेंसीकृत है  । > > इस पृष्ठ पर किए गए सभी योगदानकर्ताओं और संपादनों, पुनर्स्थापनों और अनुवादों के बारे में अधिक जानने के लिए दाएं कॉलम में प्रत्येक विकी पृष्ठ का **पृष्ठ इतिहास देखें ।** > > [योगदान](https://ko-fi.com/montessori) और [प्रायोजकों](https://ko-fi.com/montessori) का स्वागत है और बहुत सराहना की जाती है! * [मोंटेसरी विधि, दूसरा संस्करण](https://montessori-international.com/s/the-montessori-method/wiki/+Chapter+Index+-+The+Montessori+Method%2C+2nd+Edition+-+Restoration+-+Open+Library#the-montessori-method%2C-2nd-edition---restoration---open-library "मोंटेसरी क्षेत्र पर मोंटेसरी पद्धति - अंग्रेजी भाषा") - अंग्रेजी बहाली - [Archive.Org](https://archive.org/details/montessorimethod00montuoft/ "Aechive.Org . पर मोंटेसरी विधि") - [ओपन लाइब्रेरी](https://openlibrary.org/books/OL7089223M/The_Montessori_method "ओपन लाइब्रेरी पर मोंटेसरी पद्धति") * [अध्याय सूचकांक](https://montessori-international.com/s/the-montessori-method/wiki/+Chapter+Index+-+The+Montessori+Method%2C+2nd+Edition+-+Restoration+-+Open+Library) * [अध्याय 00 - समर्पण, आभार, अमेरिकी संस्करण की प्रस्तावना, परिचय](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+00+-+Dedication%2C+Acknowledgements%2C+Preface+to+the+American+Edition%2C+Introduction) * [अध्याय 01 - आधुनिक विज्ञान के संबंध में नई शिक्षाशास्त्र का एक महत्वपूर्ण विचार](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+01+-+A+critical+consideration+of+the+new+pedagogy+in+its+relation+to+modern+science) * [अध्याय 02 - विधियों का इतिहास](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+02+-+History+of+Methods) * [अध्याय 03 - "बच्चों के घरों" में से एक के उद्घाटन के अवसर पर दिया गया उद्घाटन भाषण](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+03+-+Inaugural+address+delivered+on+the+occasion+of+the+opening+of+one+of+the+%E2%80%9CChildren%E2%80%99s+Houses%E2%80%9D) * [अध्याय 04 - "बच्चों के घरों" में प्रयुक्त शैक्षणिक तरीके](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+04+-+Pedagogical+Methods+used+in+the+%E2%80%9CChildren%E2%80%99s+Houses%E2%80%9D) * [अध्याय 05 - अनुशासन](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+05+-+Discipline) * [अध्याय 06 - पाठ कैसे दिया जाना चाहिए](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+06+-+How+the+lesson+should+be+given) * [अध्याय 07 - व्यावहारिक जीवन के लिए व्यायाम](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+07+-+Exercises+for+Practical+Life) * [अध्याय 08 - बच्चे के आहार का प्रतिबिंब](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+08+-+Reflection+the+Child%E2%80%99s+diet) * [अध्याय 09 - पेशीय शिक्षा जिम्नास्टिक](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+09+-+Muscular+education+gymnastics) * [अध्याय 10 - शिक्षा में प्रकृति कृषि श्रम: पौधों और जानवरों की संस्कृति](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+10+-+Nature+in+education+agricultural+labor%3A+Culture+of+plants+and+animals) * [अध्याय 11 - कुम्हार की कला, और निर्माण के लिए मैनुअल श्रम](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+11+-+Manual+labor+the+potter%E2%80%99s+art%2C+and+building) * [अध्याय 12 - इंद्रियों की शिक्षा](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+12+-+Education+of+the+senses) * [अध्याय 13 - उपदेशात्मक सामग्री की इंद्रियों और चित्रणों की शिक्षा: सामान्य संवेदनशीलता: स्पर्शनीय, ऊष्मीय, बुनियादी, और स्टीरियो ग्नोस्टिक सेंस](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+13+-+Education+of+the+senses+and+illustrations+of+the+didactic+material%3A+General+sensibility%3A+The+tactile%2C+thermic%2C+basic%2C+and+stereo+gnostic+senses) * [अध्याय 14 - इंद्रियों की शिक्षा पर सामान्य नोट्स](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+14+-+General+notes+on+the+education+of+the+senses) * [अध्याय 15 - बौद्धिक शिक्षा](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+15+-+Intellectual+education) * [अध्याय 16 - पठन-पाठन सिखाने की विधि](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+16+-+Method+for+the+teaching+of+reading+and+writing) * [अध्याय 17 - प्रयोग की जाने वाली विधि और उपदेशात्मक सामग्री का विवरण](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+17+-+Description+of+the+method+and+didactic+material+used) * [अध्याय 18 - बचपन में भाषा](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+18+-+Language+in+childhood) * [अध्याय 19 - अंक का शिक्षण: अंकगणित का परिचय](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic) * [अध्याय 20 - अभ्यास का क्रम](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+20+-+Sequence+of+exercise) * [अध्याय 21 - अनुशासन की सामान्य समीक्षा](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+21+-+General+review+of+discipline) * [अध्याय 22 - निष्कर्ष और प्रभाव](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+22+-+Conclusions+and+impressions) * [अध्याय 23 - चित्र](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+23+-+Illustrations)