Ang Paraan ng Montessori, 2nd Edition - Pagpapanumbalik # Kabanata 19 - Pagtuturo ng pagbilang, ang pagpapakilala ng aritmetika Ang mga batang tatlong taong gulang ay alam na kung paano magbilang ng hanggang dalawa o tatlo kapag sila ay pumasok sa ating mga paaralan. Kaya't  ***napakadali***  nilang natututo ng pagbilang, na binubuo  ***sa pagbibilang ng mga bagay** .*  Ang isang dosenang iba't ibang paraan ay maaaring magsilbi patungo sa layuning ito, at ang pang-araw-araw na buhay ay nagpapakita ng maraming pagkakataon; kapag sinabi ng ina, halimbawa, "Walang dalawang butones sa iyong apron," o "Kailangan namin ng tatlo pang plato sa mesa." Isa sa mga unang paraan na ginamit ko ay ang pagbibilang gamit ang pera. Kumuha ako  ng ***bagong***  pera, at kung posible ay mayroon akong magagandang reproductions na ginawa sa karton. Nakita ko ang gayong pera na ginagamit sa isang paaralan para sa mga kulang sa London. Ang  ***paggawa ng pagbabago***  ay isang anyo ng pagbilang na kaakit-akit upang mahawakan ang atensyon ng bata. Ipinakita ko ang isa, dalawa, at apat na sentimetro na piraso, at ang mga bata, sa ganitong paraan ay natutong magbilang hanggang  ***sampu** .* Walang paraan ng pagtuturo ang mas  ***praktikal***  kaysa sa pag-iisip na gawing pamilyar ang mga bata sa mga barya na karaniwang ginagamit, at walang ehersisyo ang mas kapaki-pakinabang kaysa sa paggawa ng pagbabago. Ito ay napakalapit na nauugnay sa pang-araw-araw na buhay na ito ay interesado sa lahat ng mga bata. Ang pagkakaroon ng pagtuturo ng pagbilang sa empiric mode na ito, pumasa ako sa higit pang mga pamamaraan na pagsasanay, pagkakaroon bilang didaktikong materyal ang isa sa mga hanay ng mga bloke na ginagamit na sa edukasyon ng mga pandama; ibig sabihin, ang serye ng sampung baras na ginamit noon para sa pagtuturo ng haba. Ang pinakamaikli sa mga rod na ito ay tumutugma sa isang decimeter, ang pinakamahaba sa isang metro, habang ang mga intervening rod ay nahahati sa mga seksyon na isang decimeter ang haba. Ang mga seksyon ay pininturahan ng salit-salit na pula at asul.  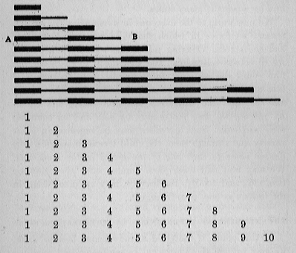Sa ibang araw, kapag inayos ng isang bata ang mga tungkod, inilalagay ang mga ito sa pagkakasunud-sunod ng haba, binibilang namin sa kanya ang pula at asul na mga palatandaan, simula sa pinakamaliit na piraso; iyon ay, isa; isa dalawa; isa, dalawa, tatlo, atbp., palaging babalik sa isa sa pagbibilang ng bawat baras, at simula sa gilid A. Pagkatapos ay pinangalanan namin ang mga solong rod mula sa pinakamaikling hanggang sa pinakamahaba, ayon sa kabuuang bilang ng mga seksyon na naglalaman ng bawat isa, hinahawakan ang mga tungkod sa gilid B, kung saang bahagi umaakyat ang hagdanan. Nagreresulta ito sa parehong pagbilang tulad ng noong binilang namin ang pinakamahabang baras 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Sa pagnanais na malaman ang bilang ng mga baras, binibilang namin ang mga ito mula sa gilid A at pareho mga resulta ng pagbilang; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Pinag-iisa na namin ngayon ang mga pagsasanay sa  ***pagbilang***  sa mga naunang pagsasanay na pandama kung saan nakilala ng bata ang mahaba at maikling mga tungkod. Ang pagkakaroon ng paghahalo ng mga tungkod sa isang karpet, ang direktor ay pumili ng isa, at ipinakita ito sa bata, ay binibilang niya ang mga seksyon; halimbawa, 5. Pagkatapos ay hiniling niya sa kanya na ibigay sa kanya ang susunod na haba. Pinipili niya ito  ***sa pamamagitan ng kanyang mata*** , at pinatunayan ng direktor ang  ***kanyang***  napili sa pamamagitan ng  ***paglalagay ng dalawang piraso sa tabi at sa pamamagitan ng pagbilang ng kanilang mga seksyon** .*  Ang ganitong mga pagsasanay ay maaaring paulit-ulit sa iba't ibang uri at sa pamamagitan ng mga ito, natututo ang bata na magtalaga ng isang  ***partikular na pangalan sa bawat isa sa mga piraso sa mahabang hagdan** .* Maaari na nating tawagan ang mga ito bilang bilang isang piraso; piraso bilang dalawa, atbp., at sa wakas, para sa maikli, ay maaaring magsalita tungkol sa mga ito sa mga aralin bilang isa, dalawa, tatlo, atbp. ## [19.1 Mga numero na kinakatawan ng mga graphic na palatandaan](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.1-numbers-as-represented-by-graphic-signs (Link sa Montessori.Zone's Translation Base Text na "The Montessori Method")) Sa puntong ito, kung alam na ng bata kung paano magsulat, maaari naming ipakita ang mga figure na pinutol sa papel de liha at inilagay sa mga card. Sa paglalahad ng mga ito, ang paraang ginagamit sa pagtuturo ng mga titik. "Ito ang isa." "Ito ay dalawa." "Bigyan mo ako ng isa." "Bigyan mo ako ng dalawa." "Anong  *numero*  ito?" Sinusubaybayan ng bata ang numero gamit ang kanyang daliri habang ginagawa niya ang mga titik. ***Mga Pagsasanay sa Mga Numero** .*  Pagsasama ng graphic sign sa dami. Nagdisenyo ako ng dalawang tray bawat isa ay nahahati sa limang maliliit na compartment. Sa likod ng bawat compartment ay maaaring ilagay ang isang card na may figure. Ang mga figure sa unang tray ay dapat na 0, 1, 2, 3, 4, at sa pangalawa, 5, 6, 7, 8, at 9. Ang ehersisyo ay halata; ito ay binubuo sa paglalagay sa loob ng mga compartment ng ilang mga bagay na naaayon sa figure na ipinahiwatig sa card sa likod ng compartment. Binibigyan namin ang mga bata ng iba't ibang bagay upang pag-iba-iba ang aralin, ngunit higit sa lahat ay gumagamit ng malalaking kahoy na pegs na napakahugis na hindi ito gumulong sa mesa. Inilalagay namin ang ilan sa mga ito sa harap ng bata na ang bahagi ay upang ayusin ang mga ito sa kanilang mga lugar, isang peg na tumutugma sa card na may markang isa, atbp. Kapag siya ay tapos na siya ay dinadala ang kanyang tray sa direktor upang ma-verify nito ang kanyang trabaho. ***Ang Aralin sa Zero** .*  Naghihintay kami hanggang sa ang bata, na itinuro ang kompartimento na naglalaman ng card na may markang zero, ay nagtanong, "At ano ang dapat kong ilagay dito?" Pagkatapos ay tumugon kami, "Wala; ang zero ay wala." Ngunit kadalasan ito ay hindi sapat. Kailangang iparamdam sa bata  ***kung ano ang ibig nating***  sabihin sa  ***wala** .*  Sa layuning ito, ginagamit namin ang mga maliliit na laro na lubos na nakakaaliw sa mga bata. Tumayo ako sa gitna nila, at bumaling sa isa sa kanila na gumamit na ng materyal na ito, sinasabi ko, "Halika, mahal, lumapit sa akin nang  ***walang***  beses." Ang bata ay halos palaging lumalapit sa akin, at pagkatapos ay tumatakbo pabalik sa kanyang lugar. "Ngunit, aking anak, dumating ka  ***minsan***  , at sinabi ko sa iyo na maging  ***zero*** ulit." Pagkatapos ay nagsimula siyang magtaka. "Ngunit ano ang dapat kong gawin, kung gayon?" "Wala; zero is nothing." "But how shall I do nothing?" "Don't do anything. Dapat kang maupo. Hindi ka dapat sumama, kahit kailan. Zero beses. Walang beses." Inuulit ko ang mga pagsasanay na ito hanggang sa maunawaan ng mga bata, at sila ay labis na nalibang sa pananatiling tahimik kapag tinatawag ko silang lumapit sa akin ng walang beses o upang halikan ako ng walang halik. Madalas silang sumisigaw, "Zero ay wala! Walang anuman si Zero!" ## [19.2 Mga pagsasanay para sa memorya ng mga numero](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.2-exercises-for-the-memory-of-numbers (Link sa Montessori.Zone's Translation Base Text na "The Montessori Method")) Kapag nakilala ng mga bata ang nakasulat na figure, at kapag ang figure na ito ay nagpapahiwatig sa kanila ng numerical value, binibigyan ko sila ng sumusunod na ehersisyo: Pinutol ko ang mga figure mula sa mga lumang kalendaryo at inilagay ang mga ito sa mga piraso ng papel na pagkatapos ay itinupi at ibinaba sa isang kahon. Inilabas ng mga bata ang mga slips at dinadala ang mga ito na nakatiklop pa rin, sa kanilang mga upuan, kung saan sila ay tumingin sa kanila at muling binalot ang mga ito,  ***na iniingatan ang sikreto** .*  Pagkatapos, isa-isa, o magkakagrupo, ang mga batang ito (na natural na pinakamatanda sa klase) ay pumunta sa malaking mesa ng direktor kung saan inilagay ang mga grupo ng iba't ibang maliliit na bagay. Pinipili ng bawat isa ang  ***dami***  ng mga bagay na tumutugma sa bilang na kanyang iginuhit. Ang numero, samantala, ay naiwan  ***sa lugar ng bata*** , isang piraso ng papel na misteryosong nakatiklop. Ang bata, samakatuwid, ay dapat  ***tandaan*** ang kanyang numero hindi lamang sa panahon ng mga paggalaw na ginagawa niya sa pagdating at pagpunta ngunit habang kinokolekta niya ang kanyang mga piraso, binibilang ang mga ito nang paisa-isa. Maaaring dito ang direktor ay gumawa ng mga interesanteng indibidwal na obserbasyon sa memorya ng numero. Kapag nakuha na ng bata ang kanyang mga bagay ay inaayos niya ang mga ito sa kanyang sariling mesa, sa dalawang hanay, at kung ang bilang ay hindi pantay, inilalagay niya ang kakaibang piraso sa ibaba at sa pagitan ng huling dalawang bagay. Samakatuwid, ang pag-aayos ng mga piraso ay ang mga sumusunod: ``` o o o o o o o o o o X XX XX XX XX XX XX XX XX XX X XX XX XX XX XX XX XX X XX XX XX XX XX X XX XX XX X XX ``` Ang mga krus ay kumakatawan sa mga bagay, habang ang bilog ay kumakatawan sa nakatiklop na slip na naglalaman ng pigura. Matapos ayusin ang kanyang mga bagay, hinihintay ng bata ang pagpapatunay. Dumating ang direktor, binuksan ang slip, binasa ang numero, at binibilang ang mga piraso. Noong una naming nilalaro ang larong ito madalas mangyari na ang mga bata ay kumuha ng  ***mas maraming bagay***  kaysa sa hinihiling sa card, at ito ay hindi palaging dahil hindi nila naaalala ang numero, ngunit nagmula sa isang kahibangan dahil sa pagkakaroon ng pinakamaraming bilang ng mga bagay. Kaunti sa likas na kasakiman na iyon, na karaniwan sa primitive at uncultured na tao. Hinahangad ng direktor na ipaliwanag sa mga bata na walang silbi na ilagay ang lahat ng mga bagay na iyon sa mesa at ang punto ng laro ay nasa pagkuha ng eksaktong bilang ng mga bagay na kailangan. Unti-unti, pumapasok sila sa ideyang ito, ngunit hindi ganoon kadali gaya ng inaakala ng isa. Ito ay isang tunay na pagsisikap ng pagtanggi sa sarili na humahawak sa bata sa loob ng itinakdang limitasyon at ginagawa siyang kumuha, halimbawa, dalawa lamang sa mga bagay na inilagay sa kanyang pagtatapon, habang nakikita niya ang iba na kumukuha ng higit pa. Ako, samakatuwid, itinuturing na ang larong ito ay higit na isang ehersisyo ng paghahangad kaysa sa pagbilang. Ang batang may  ***zero*** , ay hindi dapat gumalaw sa kanyang kinalalagyan kapag nakita niya ang lahat ng kanyang mga kasama na tumataas at malayang kumukuha ng mga bagay na hindi niya maabot. Maraming beses na nahuhulog ang zero sa kapalaran ng isang bata na marunong magbilang nang perpekto, at makakaranas ng malaking kasiyahan sa pag-iipon at pag-aayos ng isang mahusay na pangkat ng mga bagay sa tamang pagkakasunud-sunod sa kanyang mesa, at sa paghihintay nang may seguridad sa pagpapatunay ng guro. Ito ay pinaka-kagiliw-giliw na pag-aralan ang mga ekspresyon sa mga mukha ng mga taong nagtataglay ng zero. Ang mga indibidwal na pagkakaiba na nagreresulta ay halos isang paghahayag ng "karakter" ng bawat isa. Ang ilan ay nananatiling walang kibo, ipinapalagay ang isang matapang na harapan upang itago ang sakit ng pagkabigo; ang iba ay nagpapakita ng pagkabigo na ito sa pamamagitan ng hindi sinasadyang mga kilos. Gayunpaman, hindi maitatago ng iba ang ngiti na itinawag ng iisang sitwasyon kung saan nasusumpungan nila ang kanilang sarili, at na magpapa-usyoso sa kanilang mga kaibigan. May mga maliliit na sumusunod sa bawat galaw ng kanilang mga kasama na may hitsura ng pagnanasa, halos inggit, habang ang iba ay nagpapakita ng agarang pagtanggap sa sitwasyon. Hindi gaanong kawili-wili ang mga expression kung saan sila umamin sa paghawak ng zero kapag tinanong sa panahon ng pag-verify, "at ikaw, wala kang kinuha?" "May zero ako." "Ito ay zero." Ito ang mga karaniwang salita, ngunit ang nagpapahayag na mukha, at ang tono ng boses, ay nagpapakita ng malawak na iba't ibang mga damdamin. Bihira, sa katunayan, ang mga tila nagbibigay nang may kasiyahan sa pagpapaliwanag ng isang pambihirang katotohanan. Ang mas maraming bilang ay maaaring mukhang hindi masaya o nagbitiw lamang. Kami, samakatuwid, ay nagbibigay ng mga aralin sa kahulugan ng laro, na nagsasabing, "Mahirap magtago ng walang sikreto. Tiklupin nang mahigpit ang papel at huwag hayaang mawala ito. Ito ang pinakamahirap sa lahat." Sa katunayan, pagkaraan ng ilang sandali, ang napakahirap na pananatiling tahimik ay umaakit sa mga bata, at kapag binuksan nila ang slip na may markang zero ay makikita na sila ay kontento na itago ang sikreto. ## [19.3 Pagdaragdag at pagbabawas mula isa hanggang dalawampu: multiplikasyon at paghahati](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.3-addition-and-subtraction-from-one-to-twenty%3A-multiplication-and-division (Link sa Montessori.Zone's Translation Base Text na "The Montessori Method")) Ang didactic na materyal na ginagamit namin para sa pagtuturo ng mga unang aritmetika na operasyon ay pareho nang ginamit para sa pagbilang; ibig sabihin, ang mga rod ay nagtapos sa haba na, na nakaayos sa sukat ng metro, ay naglalaman ng unang ideya ng decimal system. Ang mga tungkod, gaya ng sinabi ko, ay tinawag sa pamamagitan ng mga numero na kanilang kinakatawan; isa, dalawa, tatlo, atbp. Ang mga ito ay nakaayos sa pagkakasunud-sunod ng haba, na nasa pagkakasunud-sunod din ng pagbilang. Ang unang ehersisyo ay binubuo sa pagsisikap na pagsamahin ang mas maiikling piraso sa paraang makabuo ng sampu. Ang pinakasimpleng paraan ng paggawa nito ay ang sunud-sunod na kunin ang pinakamaikling baras, mula sa isa pataas, at ilagay ang mga ito sa dulo ng kaukulang mahabang baras mula siyam pababa. Ito ay maaaring sinamahan ng mga utos, "Kunin ang isa at idagdag sa siyam; kumuha ng dalawa at idagdag sa walo; kumuha ng tatlo at idagdag sa pito; kumuha ng apat at idagdag ito sa anim." Sa ganitong paraan, gumawa kami ng apat na rod na katumbas ng sampu. Nananatili ang lima, ngunit, iniikot ito sa kanyang ulo (sa mahabang kahulugan), ito ay dumadaan mula sa isang dulo ng sampu patungo sa isa pa, at sa gayon ay nililinaw ang katotohanan na ang dalawang beses na lima ay nagiging sampu. Ang mga pagsasanay na ito ay paulit-ulit at unti-unting tinuturuan ang bata ng mas teknikal na wika; siyam kasama ang isa ay katumbas ng sampu, walo kasama ang dalawa ay katumbas ng sampu, pito at tatlo ay katumbas ng sampu, anim na kasama ang apat ay katumbas ng sampu, at para sa lima, na natitira, dalawang beses na lima ay katumbas ng sampu. Sa wakas, kung marunong siyang sumulat, itinuturo namin ang mga sign  *plus*  at  *equals*  at  *times.*  At ito ang nakikita natin sa maayos na mga note-book ng ating mga musmos: ``` 9+1=10 8+2=10 5x2=10 7+3=10 6+4=10 ``` Kapag ang lahat ng ito ay natutunang mabuti at nailagay sa papel na may labis na kasiyahan ng mga bata, tinatawag namin ang kanilang pansin sa gawaing ginagawa kapag ang mga piraso na pinagsama-sama upang bumuo ng sampu ay pinaghiwa-hiwalay at ibinalik sa kanilang orihinal na mga posisyon. Mula sa sampung huling nabuo inalis namin ang apat at anim na labi; mula sa susunod, inaalis namin ang tatlo at pitong labi; mula sa susunod, dalawa at walo ang natitira; mula sa huli, inaalis namin ang isa at siyam na labi. Sa pagsasalita tungkol dito nang maayos ang sinasabi natin, sampu mas mababa sa apat ay katumbas ng anim; sampu mas mababa sa tatlo ay katumbas ng pito; sampung mas mababa sa dalawa ay katumbas ng walo; sampung mas mababa ang isa ay katumbas ng siyam. Tungkol sa natitirang lima, ito ay kalahati ng sampu, at sa pamamagitan ng pagputol ng mahabang baras sa dalawa, iyon ay paghahati ng sampu sa dalawa, magkakaroon tayo ng lima; sampu na hinati sa dalawa ay katumbas ng lima. Ang nakasulat na rekord ng lahat ng ito ay mababasa: ``` 10-4=6 10-3=7 10 / 2=5 10-2=8 10-1=9 ``` Kapag ang mga bata ay nakabisado na ang pagsasanay na ito, sila ay kusang nagpaparami nito. Maaari ba tayong gumawa ng tatlo sa dalawang paraan? Inilalagay natin ang isa pagkatapos ng dalawa at pagkatapos ay isusulat, upang maalala natin ang ating ginawa, 2+1=3. Maaari ba tayong gumawa ng dalawang baras na katumbas ng bilang na apat? 3+1=4, at 4-3=1; 4-1=3. Ang rod number two sa kaugnayan nito sa rod number four ay itinuturing bilang lima na may kaugnayan sa sampu; ibig sabihin, ibinabalik natin ito at ipinapakita na ito ay nakapaloob sa apat na eksaktong dalawang beses: 4/2=2; 2x2=4. Isa pang problema: tingnan natin kung ilang rod ang maaari nating laruin sa parehong laro. Magagawa natin ito sa tatlo at anim, at sa apat at walo; yan ay, ``` 2x2=4 3x2=6 4x2=8 5x2=10 10/2=5 8/2=4 6/2=3 4/2=2 ``` Sa puntong ito nalaman namin na ang mga cube kung saan namin nilalaro ang mga number memory game ay makakatulong:  Mula sa pag-aayos na ito, makikita ng isa nang sabay-sabay kung alin ang mga numero na maaaring hatiin ng dalawa ang lahat ng walang kakaibang kubo sa ibaba. Ito ang mga  ***even***  na numero dahil maaari silang ayusin nang pares, dalawa sa dalawa; at ang paghahati sa dalawa ay madali, ang kailangan lang ay paghiwalayin ang dalawang linya ng dalawa na nakatayo sa ilalim ng isa. Ang pagbibilang ng mga cube ng bawat file ay mayroon kaming quotient. Upang i-recompose ang primitive na numero kailangan lang nating i-reassemble ang dalawang file kaya 2x3=6. Ang lahat ng ito ay hindi mahirap para sa mga batang limang taong gulang. Ang pag-uulit sa lalong madaling panahon ay nagiging walang pagbabago, ngunit ang mga pagsasanay ay maaaring pinakamadaling baguhin, kunin muli ang hanay ng mga mahabang baras, at sa halip na ilagay ang baras bilang isa pagkatapos ng siyam, ilagay ito pagkatapos ng sampu. Sa parehong paraan, ilagay ang dalawa pagkatapos ng siyam, at tatlo pagkatapos ng walo. Sa ganitong paraan gumawa kami ng mga tungkod na mas malaki kaysa sampu; mga haba na dapat nating matutunang pangalanan ang labing-isa, labindalawa, labintatlo, atbp., hanggang dalawampu. Ang maliit na cube, masyadong, ay maaaring gamitin upang ayusin ang mas mataas na mga numerong ito Ang pagkakaroon ng natutunan ang mga operasyon sa pamamagitan ng sampu, magpatuloy kami nang walang kahirapan sa dalawampu't. Ang isang kahirapan ay nakasalalay sa mga  ***decimal na numero***  na nangangailangan ng ilang mga aralin. ## [19.4 Mga aralin sa mga decimal: mga pagkalkula ng arithmetical na lampas sa sampu](https://montessori-international.com/s/the-montessori-method/wiki/Chapter+19+-+Teaching+of+numeration%3A+Introduction+to+arithmetic#19.4-lessons-on-decimals%3A-arithmetical-calculations-beyond-ten (Link sa Montessori.Zone's Translation Base Text na "The Montessori Method")) Ang kinakailangang materyal na didactic ay binubuo ng isang bilang ng mga square card kung saan ang figure sampu ay naka-print sa malaking uri, at ng iba pang mga rectangular card, kalahati ng laki ng square, at naglalaman ng mga solong numero mula isa hanggang siyam. Inilalagay namin ang mga numero sa isang linya; 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Pagkatapos, kapag wala nang mga numero, kailangan nating magsimulang muli at kunin muli ang 1. Ang 1 na ito ay katulad ng seksyong iyon sa hanay ng mga baras na, sa numero ng baras 10, ay umaabot nang lampas sa siyam. Nagbibilang  ***sa hagdan*** hanggang siyam, nananatili itong isang seksyon na, dahil wala nang mga numero, muli naming itinalaga bilang 1; ngunit ito ay isang mas mataas na 1 kaysa sa una, at upang makilala ito mula sa una ay inilalagay namin malapit dito ang isang sero, isang palatandaan na walang ibig sabihin. Narito kung gayon ang 10. Sinasaklaw ang zero gamit ang hiwalay na mga parihabang numero ng card sa pagkakasunud-sunod ng kanilang pagkakasunod-sunod na nakikita nating nabuo: 11, 12, 13, 14, 15, 16, 17, 18, 19. Ang mga numerong ito ay binubuo sa pamamagitan ng pagdaragdag sa rod number 10, first-rod number 1, then 2, then 3, etc., hanggang sa wakas ay idagdag natin ang rod number 9 sa rod number 10, sa gayon ay nakakakuha ng napakahabang rod, na, kapag nagpalitan ito ng pula at asul na mga seksyon ay binibilang, ay nagbibigay kami labing siyam.  Maaaring ipakita ng direktor sa bata ang mga card, na nagbibigay ng numero 16, at maaari niyang ilagay ang rod 6 pagkatapos ng rod 10. Pagkatapos ay inalis niya ang card na may 6, at inilalagay sa ibabaw ng zero ang card na may figure na 8, kung saan ang bata inalis ang baras 6 at pinapalitan ito ng baras 8, kaya nagiging 18. Ang bawat isa sa mga kilos na ito ay maaaring itala nang ganito: 10+6=16; 10+8=18, atbp. Nagpapatuloy kami sa parehong paraan sa pagbabawas. 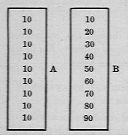Kapag ang numero mismo ay nagsimulang magkaroon ng malinaw na kahulugan sa bata, ang mga kumbinasyon ay ginawa sa isang mahabang card, inaayos ang mga parihabang card na may siyam na mga numero sa dalawang hanay ng mga numero na ipinapakita sa figure A at B. Sa card A ay ipinapatong namin sa zero ng pangalawang 10, ang hugis-parihaba na card na may 1: at sa ilalim nito ang isa na may dalawa, atbp. Kaya habang ang isa sa sampu ay nananatiling pareho ang mga numero sa kanan ay nagpapatuloy mula sa zero hanggang siyam, kaya:  Sa card B ang mga aplikasyon ay mas kumplikado. Ang mga card ay nakapatong sa numerical progression ng sampu. Halos lahat ng aming mga anak ay bumibilang hanggang 100, isang numero na ibinigay sa kanila bilang tugon sa ipinakita nilang pagkamausisa tungkol sa pag-aaral nito. Hindi ako naniniwala na ang yugtong ito ng pagtuturo ay nangangailangan ng karagdagang mga paglalarawan. Maaaring paramihin ng bawat guro ang mga praktikal na pagsasanay sa mga operasyong arithmetical, gamit ang mga simpleng bagay na madaling hawakan at hatiin ng mga bata. > ##### **Ang Lisensya ng pahinang ito:** > > Ang pahinang ito ay bahagi ng “ **Montessori Restoration and Translation Project** ”.\ > Mangyaring [suportahan ang](https://ko-fi.com/montessori) aming " **All-Inclusive Montessori Education for All 0-100+ Worldwide** " inisyatiba. Lumilikha kami ng bukas, libre, at abot-kayang mapagkukunan na magagamit para sa lahat ng interesado sa Montessori Education. Binabago namin ang mga tao at kapaligiran upang maging tunay na Montessori sa buong mundo. Salamat! > > [](http://creativecommons.org/licenses/by-nc-sa/4.0/) > > **Lisensya:** Ang gawaing ito kasama ang lahat ng mga pag-edit at pagsasalin sa pagpapanumbalik nito ay lisensyado sa ilalim ng  [Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License](http://creativecommons.org/licenses/by-nc-sa/4.0/) . > > Tingnan ang **Kasaysayan** ng Pahina ng bawat pahina ng wiki sa kanang column upang matuto nang higit pa tungkol sa lahat ng mga nag-ambag at pag-edit, pagpapanumbalik, at pagsasalin na ginawa sa pahinang ito. > > [Ang mga kontribusyon](https://ko-fi.com/montessori) at [Sponsor](https://ko-fi.com/montessori) ay malugod na tinatanggap at lubos na pinahahalagahan! * [Ang Montessori Method, 2nd Edition](https://montessori-international.com/s/the-montessori-method/wiki/Filipino "Ang Montessori Method sa Montessori Zone - English Language") - Pagpapanumbalik ng Filipino - [Archive.Org](https://archive.org/details/montessorimethod00montuoft/ "Ang Montessori Method sa Aechive.Org") - [Open Library](https://openlibrary.org/books/OL7089223M/The_Montessori_method "Ang Montessori Method sa Open Library") * [0 - Index ng Kabanata - Ang Paraan ng Montessori, 2nd Edition - Pagpapanumbalik - Open Library](https://montessori-international.com/s/the-montessori-method/wiki/0+-+Index+ng+Kabanata+-+Ang+Paraan+ng+Montessori%2C+2nd+Edition+-+Pagpapanumbalik+-+Open+Library) * [Kabanata 00 - Dedikasyon, Mga Pagkilala, Paunang Salita sa American Edition, Panimula](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+00+-+Dedikasyon%2C+Mga+Pagkilala%2C+Paunang+Salita+sa+American+Edition%2C+Panimula) * [Kabanata 01 - Isang kritikal na pagsasaalang-alang ng bagong pedagogy sa kaugnayan nito sa modernong agham](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+01+-+Isang+kritikal+na+pagsasaalang-alang+ng+bagong+pedagogy+sa+kaugnayan+nito+sa+modernong+agham) * [Kabanata 02 - Kasaysayan ng Mga Paraan](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+02+-+Kasaysayan+ng+Mga+Paraan) * [Kabanata 03 - Inaugural na talumpati na ibinigay sa okasyon ng pagbubukas ng isa sa "Mga Bahay ng mga Bata"](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+03+-+Inaugural+na+talumpati+na+ibinigay+sa+okasyon+ng+pagbubukas+ng+isa+sa+%22Mga+Bahay+ng+mga+Bata%22) * [Kabanata 04 - Mga Pamamaraang Pedagogical na ginamit sa "Mga Bahay ng mga Bata"](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+04+-+Mga+Pamamaraang+Pedagogical+na+ginamit+sa+%22Mga+Bahay+ng+mga+Bata%22) * [Kabanata 05 - Disiplina](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+05+-+Disiplina) * [Kabanata 06 - Paano dapat ibigay ang aralin](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+06+-+Paano+dapat+ibigay+ang+aralin) * [Kabanata 07 - Mga Pagsasanay para sa Praktikal na Buhay](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+07+-+Mga+Pagsasanay+para+sa+Praktikal+na+Buhay) * [Kabanata 08 - Pagnilayan ang diyeta ng Bata](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+08+-+Pagnilayan+ang+diyeta+ng+Bata) * [Kabanata 09 - Muscular education gymnastics](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+09+-+Muscular+education+gymnastics) * [Kabanata 10 - Kalikasan sa edukasyon agricultural labor: Kultura ng mga halaman at hayop](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+10+-+Kalikasan+sa+edukasyon+agricultural+labor%3A+Kultura+ng+mga+halaman+at+hayop) * [Kabanata 11 - Manu-manong paggawa ng sining ng magpapalayok, at gusali](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+11+-+Manu-manong+paggawa+ng+sining+ng+magpapalayok%2C+at+gusali) * [Kabanata 12 - Edukasyon ng mga pandama](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+12+-+Edukasyon+ng+mga+pandama) * [Kabanata 13 - Edukasyon ng mga pandama at paglalarawan ng materyal na didaktiko: Pangkalahatang sensibilidad: Ang pandamdam, thermic, basic, at stereo gnostic na pandama](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+13+-+Edukasyon+ng+mga+pandama+at+paglalarawan+ng+materyal+na+didaktiko%3A+Pangkalahatang+sensibilidad%3A+Ang+pandamdam%2C+thermic%2C+basic%2C+at+stereo+gnostic+na+pandama) * [Kabanata 14 - Pangkalahatang mga tala sa edukasyon ng mga pandama](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+14+-+Pangkalahatang+mga+tala+sa+edukasyon+ng+mga+pandama) * [Kabanata 15 - Edukasyong intelektwal](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+15+-+Edukasyong+intelektwal) * [Kabanata 16 - Paraan para sa pagtuturo ng pagbasa at pagsulat](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+16+-+Paraan+para+sa+pagtuturo+ng+pagbasa+at+pagsulat) * [Kabanata 17 - Paglalarawan ng pamamaraan at didaktikong materyal na ginamit](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+17+-+Paglalarawan+ng+pamamaraan+at+didaktikong+materyal+na+ginamit) * [Kabanata 18 - Wika sa pagkabata](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+18+-+Wika+sa+pagkabata) * [Kabanata 19 - Pagtuturo ng pagbilang: Panimula sa aritmetika](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+19+-+Pagtuturo+ng+pagbilang%3A+Panimula+sa+aritmetika) * [Kabanata 20 - Pagkakasunod-sunod ng ehersisyo](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+20+-+Pagkakasunod-sunod+ng+ehersisyo) * [Kabanata 21 - Pangkalahatang pagsusuri ng disiplina](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+21+-+Pangkalahatang+pagsusuri+ng+disiplina) * [Kabanata 22 - Mga konklusyon at impresyon](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+22+-+Mga+konklusyon+at+impresyon) * [Kabanata 23 - Mga Ilustrasyon](https://montessori-international.com/s/the-montessori-method/wiki/Kabanata+23+-+Mga+Ilustrasyon)